Context
In Structural Health Monitoring (SHM), we want to automatically detect defects/damages on a structure in order to perform interventions. Usually the focus of SHM is the detection of changes in the modal characteristics of structures (i.e. eigenmodes and eigenvalues of the system). However, in order for a damage to influence the modal characteristics of a structure, it has to be quite significant. On the other hand, local strain concentrations occur even for the slightest defect or inhomogeneity under certain loading conditions.
Although this approach is promising, there are certain limitations:
- Certain loading conditions (and sensor positions/orientations) cannot be used to localize a crack (we have ambiguity/uncertainty on localization)
- it is not easy to consistently reason about the spatial variations of strain tensors w.r.t. defect positions, so hand-engineering features for localization is hard, therefore we want a fully data-driven method
- assuming we have discrete sensors, it is not clear how to learn a function that can jointly take into account the stress tensor time-series at arbitrary positions by exploiting the relative positioning of the sensors to learn spatial patterns.
In order to deal with the arbitrary positioning of sensors, it is better to think in terms of learning functions that depend on the relative position of sensors. This is where Graph Neural Networks (GraphNets) come into play. GraphNets implement learnable message passing on static graphs that implement inductive biases. The inductive biases in this work are the following:
- effect of strain is spatially local (implemented by defining a graph through spatial locallity of sensors)
- Information from several sensors needs to be used to detect spatial crack related patterns on a strain-field
- The relative position of each pair of sensors is important.
The 3rd point is important also for correctly taking into account the strain tensor readings. The strain tensor is not rotationally invariant, therefore it’s important to incorporate orientation information.
Here is a simulation of the strain patterns for a structure containing a crack:
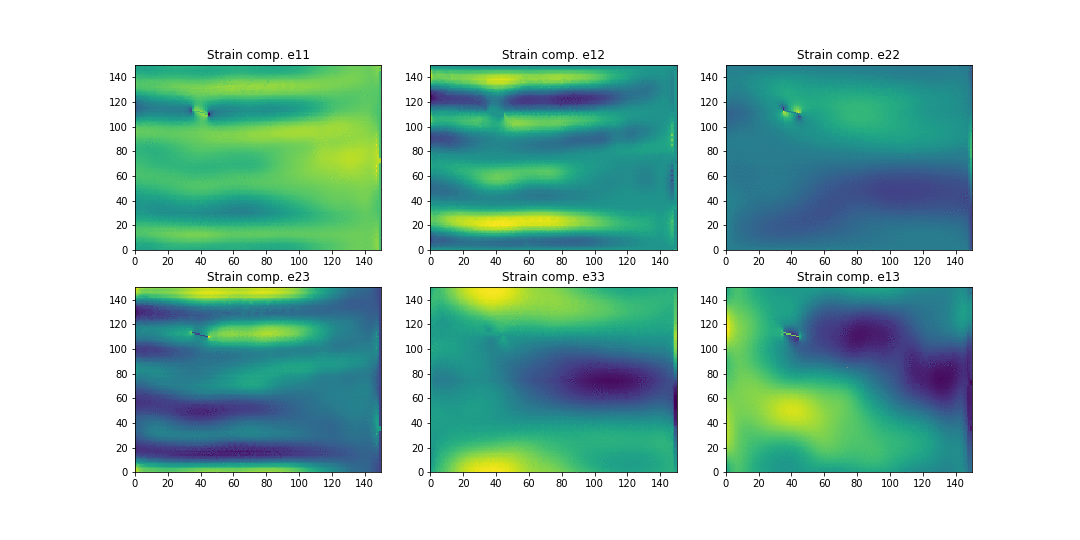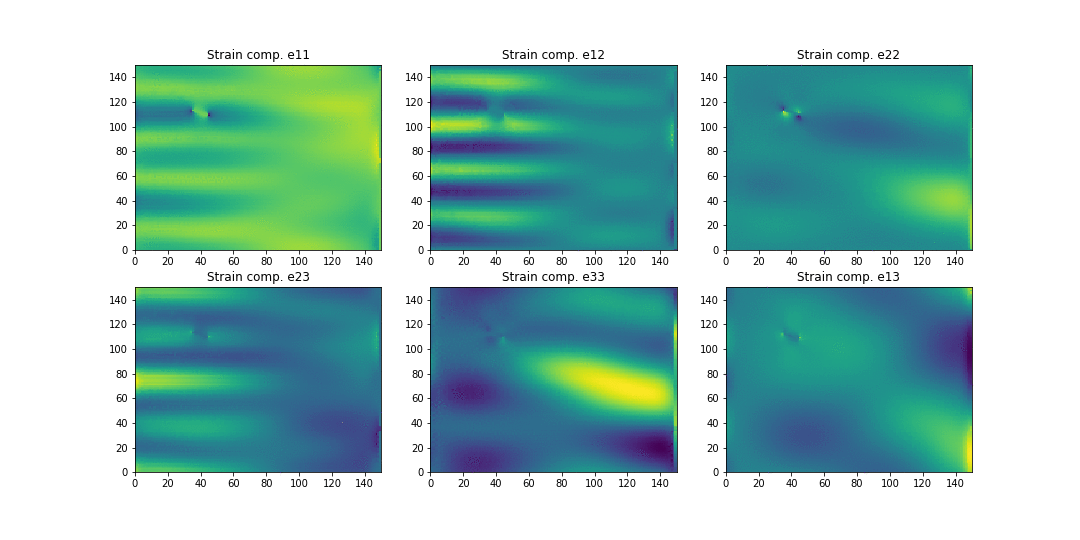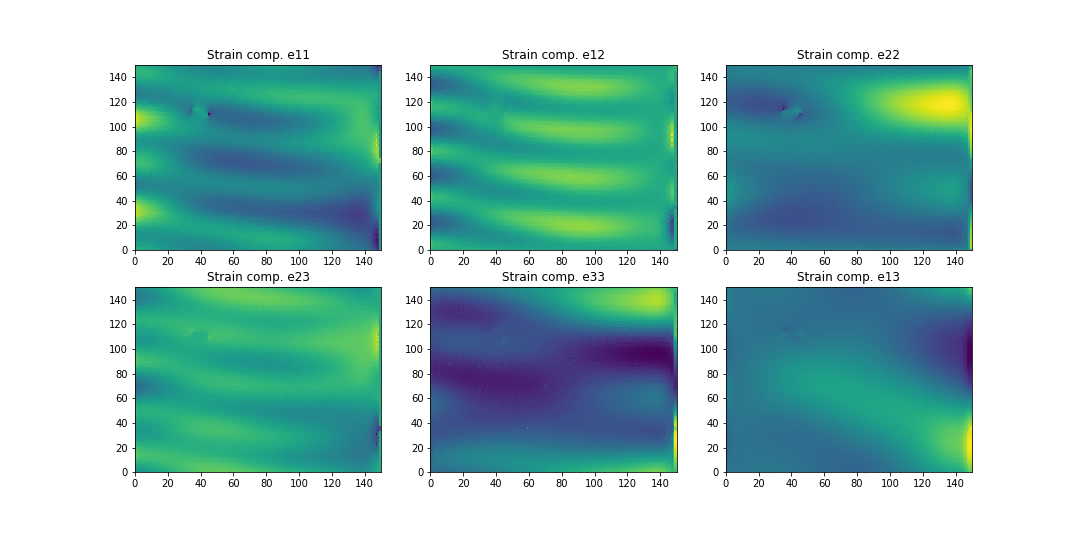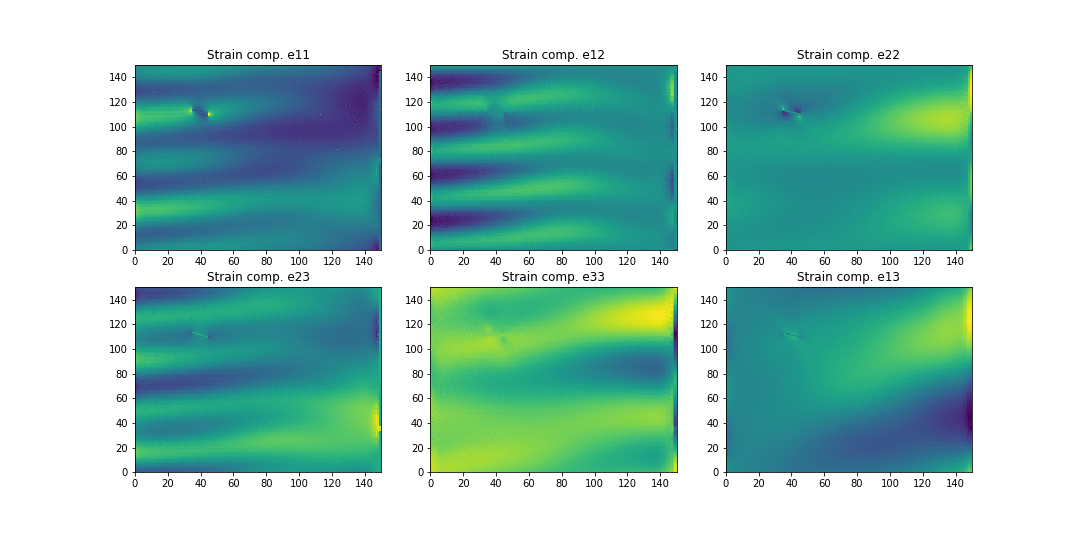
This corresponds to a randomly loaded tube supported in one end (right) with a single crack. The different plots correspond to the 6 different components of the strain tensor.
Dealing with Uncertainty
The strain-based crack localization problem is, in general, ill-posed (as many inverse problems). One of the reasons this problem is ill-posed, is because there are strain patterns that can correspond to different defects (even for a single crack) therefore ambiguity on the defect position may exist. Moreover, when learning on real data, there is inevitable noise in the measurements which will not allow for complete determination of the functions that transform the strain readings to crack positions. In order to deal with this issue, weight uncertainty on the learned GraphNet functions was used. The additive local reparametrization trick for variational Bayes was used. The following figure summarizes the approximations used:
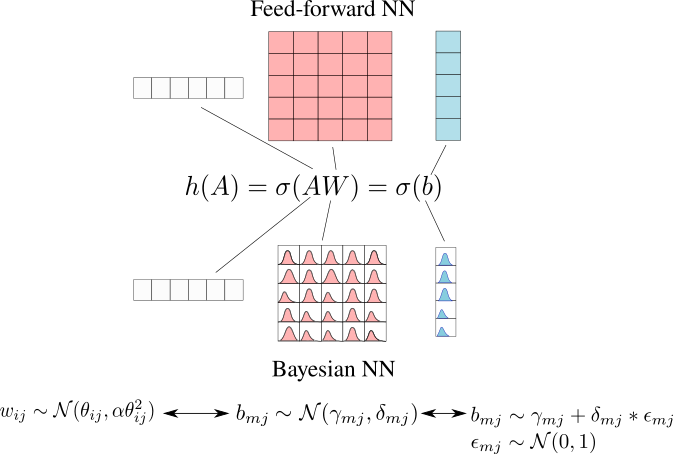
Essentially, this is a VAE-type reparametrization of the activations of a layer (and a corresponding modification to the loss function) that also takes advantage of the fact that instead of modeling the weights with a gaussian we can model the pre-activations with a gaussian. I highly recommend this lecture on the subject if you would like to learn more. In my conference paper the application of the above (GNNs + BNNs) is demonstrated on a simulated dataset for the problem of strain-based crack detection.
GNN implementation:
I have been developing my own GNN library to be able to implement my ideas faster without the constraints of DeepMind’s or Microsoft’s existing libraries. If you’re interested have a look at my repository mylonasc/tf-gnns.